Xbar R Charts with SigmaXL

What is an Xbar R Chart with SigmaXL?

The Xbar R chart with SigmaXL is a control chart for continuous data with a constant subgroup size between two and ten.

• The Xbar chart plots the average of a subgroup as a data point.
• The R chart plots the difference between the highest and lowest values within a subgroup as a data point.

The Xbar chart monitors the process mean and the R chart monitors the variation within subgroups. The Xbar is valid only if the R chart is in control.
The underlying distribution of the Xbar-R chart is normal distribution.

Plot and Xbar R Chart with SigmaXL

Data File: “Xbar-R” tab in “Sample Data.xlsx”

Steps to plot an Xbar R chart with SigmaXL:

1. Select the entire range of the data
2. Click SigmaXL -> Control Charts -> X-Bar & R
3. A new window named “X-Bar & R” appears with the selected range automatically populated into the box below “Please select your data”.
   
4. Click “Next>>”
5. A new window named “X-Bar and Range Chart” pops up.
6. Select the “Measurement” as the “Numeric Data Variables (Y)”
   Select the “Subgroup ID” as the “Subgroup Column or Size”
7. Check the checkbox of “Tests for Special Causes”
   
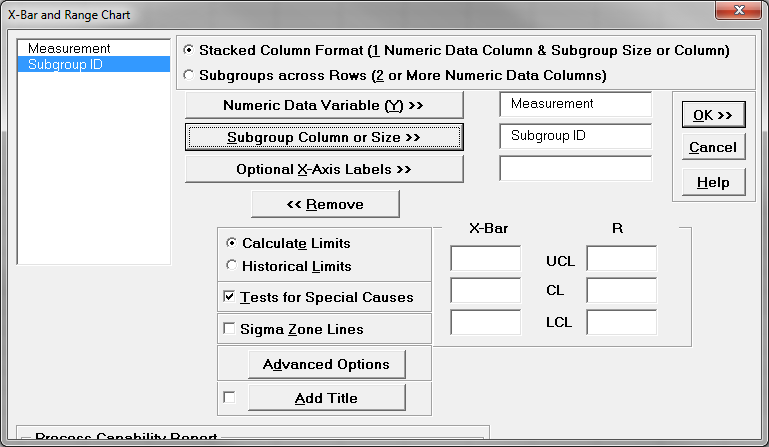
8. Click “OK>>”
9. The Xbar-R charts appear in the newly generated tab “Indiv & MR Charts (1)”.
   

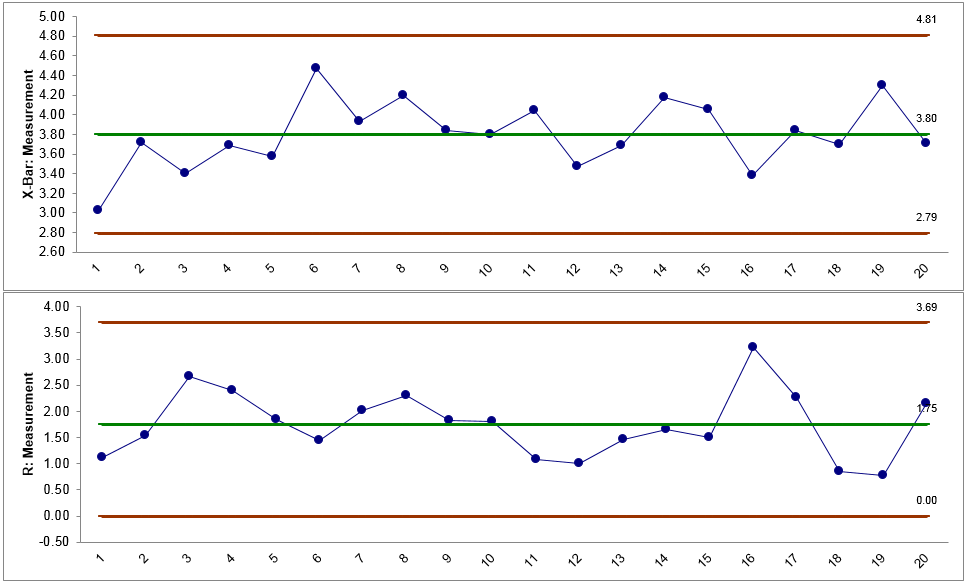
Xbar-R Charts Diagnosis

Model summary: Since the R chart is in control, the Xbar chart is valid and no points on the Xbar chart are out of control. In both charts, there are not any data points failing any tests for special causes (i.e., all the data points fall between the control limits and spread around the center line with a random pattern). We conclude that the process is in control.