Two Sample t Test with SigmaXL

What is a Two Sample t Test with SimgaXL

Two sample t test is a hypothesis test to study whether there is a statistically significant difference between the means of two populations.

• Null Hypothesis (H0): μ1 = μ2
• Alternative Hypothesis (Ha): μ1 ≠ μ2

Where: μ1 is the mean of one population and μ2 is the mean of the other population of our interest.

Assumptions of Two Sample T Tests

The sample data drawn from both populations are unbiased and representative.
The data of both populations are continuous.
The data of both populations are normally distributed.
The variances of both populations are unknown.
Two sample t-test is more robust than a z-test when the sample size is small (< 30).

Three Types of Two Sample T Tests

• Two sample t test when the variances of two populations are unknown but equal
• Two sample t test (when σ21 = σ22)
• Two sample t test when the variances of the two population are unknown and unequal
• Two sample t test (when σ21 ≠ σ22)
• Paired t-test when the two populations are dependent of each other, so each data point from one distribution corresponds to a data point in the other distribution.

Test of Equal Variance

To check whether the variances of two populations of interest are statistically significant different, we use the test of equal variance.

• Null Hypothesis (H0): σ_1^2=σ_2^2
• Alternative Hypothesis (H1): σ_1^2≠σ_2^2

An F-test is used to test the equality of variances between two normally distributed populations.
An F-test is a statistic hypothesis test in which the test statistic follows an F-distribution when the null hypothesis is true. The most known F-test is the test of equal variance for two normally distributed populations. The F-test is very sensitive to non-normality. When any one of the two populations is not normal, we use the Brown–Forsythe test for checking the equality of variances.

Decision Rules of a Two Sample T Test

• Null Hypothesis (H0): μ1 = μ2
• Alternative Hypothesis (Ha): μ1 ≠ μ2

If |tcalc| > tcrit, we reject the null and claim there is a statistically significant difference between the means of the two populations.
If |tcalc| < tcrit, we fail to reject the null and claim there is not any statistically significant difference between the means of the two populations.

Run a Two-Sample T Test with Minitab

Case study: We are trying to compare the average retail price of a product in state A and state B.
Data File: “Two-Sample T-Test” tab in “Sample Data.xlsx”

• Null Hypothesis (H0): μ1 = μ2
• Alternative Hypothesis (Ha): μ1 ≠ μ2

In this example we will be comparing the average price of a product in two different states. The null hypothesis is that the price in state A is equal to the price in state B.

Step 1: Test the normality of the retail price for both state A and B.

1. Select the entire range of data (both State and Retail Price)
2. Click SigmaXL -> Graphical Tools -> Histogram & Descriptive Statistics
3. A window named “Histogram & Descriptive” pops up with the selected range pre-populated in the box below “Please select your data”
   
4. Click “Next >>”
5. Another window named “Histogram & Descriptive Statistics” appears
6. Select “Retail Price” as the “Numeric Data Variables”
7. Select “State” as the “Group Category (X1)”
   
8. Click “OK>>”
9. The normality test results appear in the tab “Hist Descript (1)” automatically.
   
   

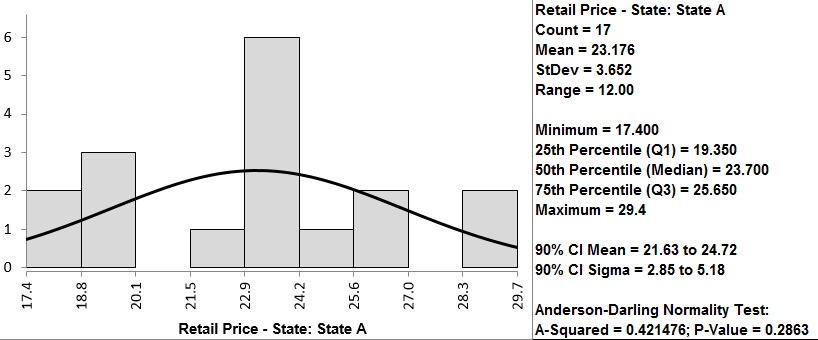
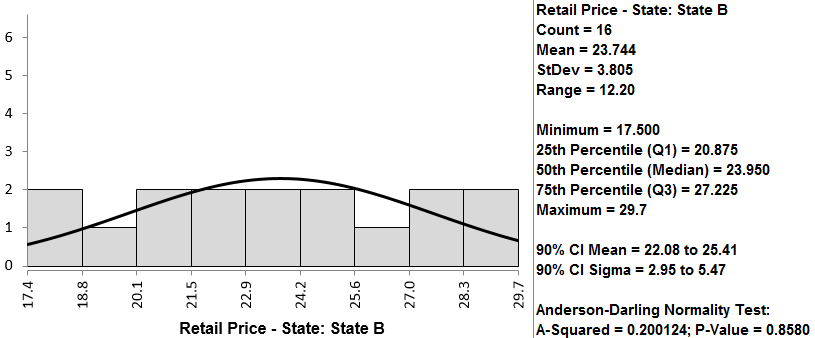
Both retail price data of state A and B are normally distributed since the p-values are both greater than alpha level (0.05). If any of the data series is not normally distributed, we need to use another hypothesis testing method other than the two-sample t-test.

By following the instructions on the previous page, we first determine if the data follow a normal distribution. In this case, you can see that the p-value for both is higher than 0.05, so we fail to reject the null hypothesis that the data are normally distributed. If the data are not normally distributed, we must use a different test.

Step 2: Test whether the variances of the two data sets are equal.

• Null Hypothesis(H₀):
• Alternative Hypothesis(H_a):

Because the retail prices at state A and state B are both normally distributed, an F test is used to test their variance equality. The p-value of F test is 0.870, greater than the alpha level (0.05), so we fail to reject the null hypothesis and we claim that the variances of the two data sets are equal. We will use the two-sample t-test (when σ²₁ = σ²₂) to compare the means of the two groups. If σ²₁ ≠ σ²₂, we will use the two-sample t-test (when σ²₁ ≠ σ²₂) to compare the means of the two groups.

Step 2: Test whether the variances of the two data sets are equal.

1. Select the entire range of data (both “State” and “Retail Price”)
2. Click SigmaXL -> Statistical Tools -> 2 Sample Comparison Tests
3. A new window named “2 Sample Comp Test” pops up with the selected range pre-populated in the box under “Please select your data”.
   
4. Click “Next>>”
5. Another window named “2 Sample Comparison Test” appears
6. Click the radio button “Stacked Column Format (1 Numeric Data Column & 1 Group Category Column)
7. Select “Retail Price” as the “Numeric Data Variable (Y)”
   Select “State” as the “Group Category (X)”
   
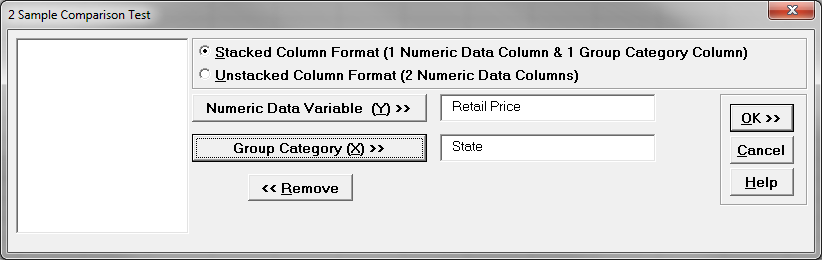
8. Click “OK>>”
9. The results show up in the tab “2 Sample Comparison Test (1)”
   

Step 3: Run two-sample t-test to compare the means of two groups.

The two-sample comparison test we ran in step 2 also automatically generate the two-sample t-test result. Therefore, we do not need to demonstrate the steps to run the Two-Sample t, we’ll use this output to interpret the results.

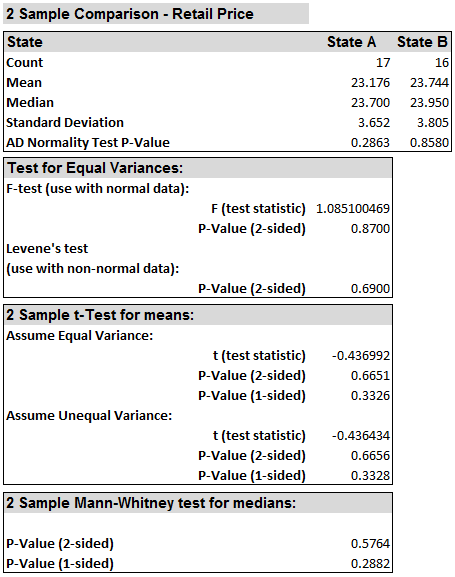Model summary: Since the p-value of the two-sided t-test (assuming equal variance) is 0.665, greater than the alpha level (0.05), we fail to reject the null hypothesis and we claim that the means of the two data sets are equal. If the variances of the two groups do not equal, we will need to use the two-sample t-test (when σ₁ ≠ σ₂) to compare the means of the two groups.

Since the p-value of the t-test (assuming unequal variance) is 0.666, greater than the alpha level (0.05), we fail to reject the null hypothesis and we claim that the means of two groups are equal.