Two Sample Proportion Test with JMP

What is the Two Sample Proportion Test?

The two sample proportion test is a hypothesis test to compare the proportions of one certain event occurring in two populations following the binomial distribution.

Null Hypothesis(H₀): p₁ = p₂
Alternative Hypothesis(H_a): p₁ ≠ p₂

Two Sample Proportion Test Assumptions

The sample data drawn from the populations of interest are unbiased and representative
There are only two possible outcomes in each trial for both populations: success/failure, yes/no, and defective/non-defective etc.
The underlying distributions of both populations are binomial distribution
When np ≥ 5 and np(1 – p) ≥ 5, the binomial distribution can be approximated by the normal distribution

How the Two Sample Proportion Test Works

When np ≥ 5 and np(1 – p) ≥ 5, we use normal distribution to approximate the underlying binomial distributions of the populations.
Test Statistic

Where:

Two Sample Proportion MTB_a

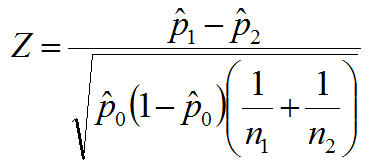
and where:

Two Sample Proportion MTB_b

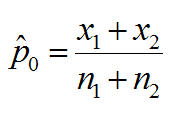
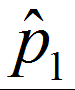and 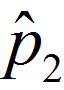are the observed proportions of events in the two samples
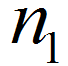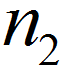and is the number of trials in the two samples respectively
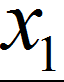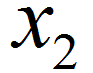and is the number of events in the two samples respectively

When |Z_calc| is smaller than Z_crit, , we fail to reject the null hypothesis.

Use JMP to Run a Two Sample Proportion Test

Case study: We are interested in comparing the exam pass rates of a high school in March and April using a nonparametric (i.e. distribution-free) hypothesis test: two sample proportion test.
Data File:“TwoSampleProportion.jmp”

Two Sample Proportion JMP_1.0

Null Hypothesis(H₀): p_March = p_April
Alternative Hypothesis(H_a): p_March ≠ p_April

Steps to run a two sample proportion test in JMP:

Click Analyze -> Fit Y by X
Select “Results” as “Y, Responses”
Select “Month” as “X, Factor”
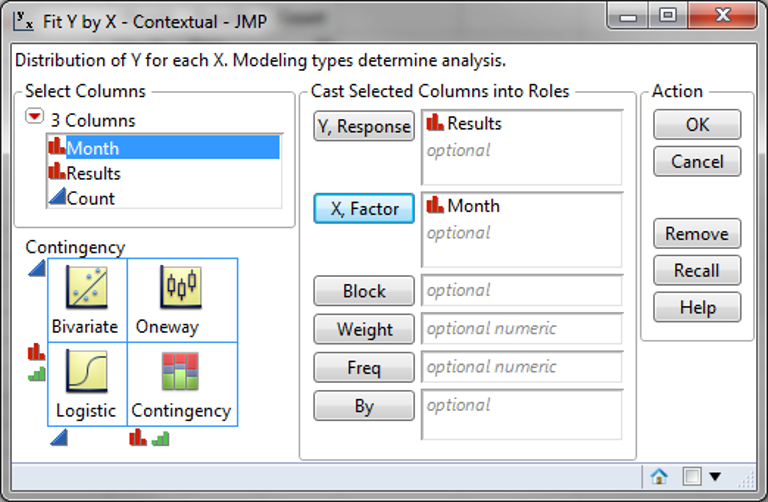
Click “OK”

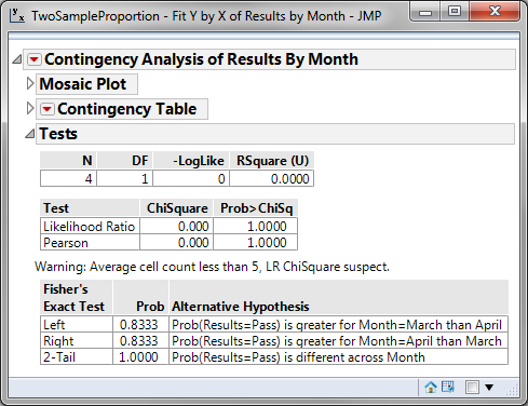
Model summary: The p-value of the two sample proportion test is 0.849, greater than the alpha level (0.05), and we fail to reject the null hypothesis. We conclude that the exam pass rates of the high school in March and April are not statistically different. In the output from the test we see the p-value is higher than the alpha value of 0.05; therefore, we fail to reject the null hypothesis and claim there is not a difference between the school’s exam pass rate in March and April.

Lean Sigma Corporation

Lean Sigma Corporation is a trusted leader in Lean Six Sigma training and certification, boasting a rich history of providing high-quality educational resources. With a mission to honor and maintain the traditional Lean Six Sigma curriculum and certification standards, Lean Sigma Corporation has empowered thousands of professionals and organizations worldwide with over 5,300 certifications, solidifying its position and reputation as a go-to source for excellence through Lean Six Sigma methodologies.

See Full Bio