One Sample Proportion Test with Minitab

What is the One Sample Proportion Test?

One sample proportion test is a hypothesis test to compare the proportion of one certain outcome (e.g. the number of successes per the number of trials, or the number of defects per the total number of opportunities) occurring in a population following the binomial distribution with a specified proportion.

• Null Hypothesis (H₀): p = p₀
• Alternative Hypothesis (H_a): p ≠ p₀

One Sample Proportion Test Assumptions

• The sample data drawn from the population of interest are unbiased and representative.
• There are only two possible outcomes in each trial: success/failure, yes/no, and defective/non-defective etc.
• The underlying distribution of the population is binomial distribution.
• When np ≥ 5 and np(1 – p) ≥ 5, the binomial distribution can be approximated by the normal distribution.

How the One Sample Proportion Test Works

When np ≥ 5 and np(1 – p) ≥ 5, we use normal distribution to approximate the underlying binomial distribution of the population.
Test Statistic

Where:

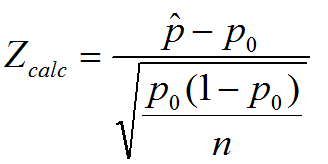
• p ̂  is the observed probability of one certain outcome occurring
• p₀ is the hypothesized probability
• n is the number of trials.
• When |Zcalc| (absolute value of the calculated test statistic) is smaller than Zcrit (critical value), we fail to reject the null hypothesis and claim that there is no statistically significant difference between the population proportion and the hypothesized proportion.

Use Minitab to Run a One Sample Proportion Test

Case study: We are interested in comparing the exam pass rate of a high school this month against a specified rate (70%) using a nonparametric (i.e. distribution-free) hypothesis test: one sample proportion test.
Data File: “One Sample Proportion” tab in “Sample Data.xlsx”

• Null Hypothesis (H₀): p = 70%
• Alternative Hypothesis (H_a): p ≠ 70%

Steps to run a one sample proportion test in Minitab:

1. Click Stat → Basic Statistics → 1 Proportion.
2. A new window named “One-SampleProportion” appears.
3. Click on the drop-down menu and choose “Summarized data.”
4. Enter “77” in the box of “Number of events.”
5. Enter “105” in the box of “Number of trials.”
6. Check the box “Perform hypothesis test.”
7. Enter “0.70” as the “Hypothesized proportion.”
   
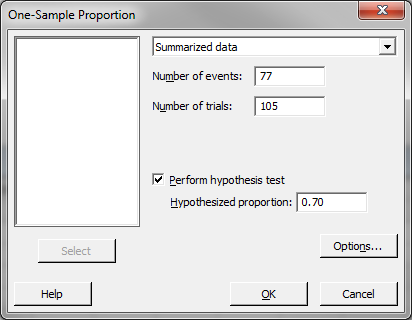
8. Click “OK.”
9. The one sample proportion test results appear in the session window.
   

Model summary: The p-value of the one sample proportion test is 0.460, greater than the alpha level (0.05), and we fail to reject the null hypothesis. We conclude that the exam pass rate of the high school this month is not statistically different from 70%.