CumSum Chart with JMP

What is a CumSum Chart?

The CumSum chart (also called cumulative sum control chart or CUMSUM chart) is a control chart of monitoring the cumulative sum of the subgroup mean deviations from the process target. It detects the shift of the process mean from the process target over time. The underlying distribution of the CumSum chart is normal distribution.
There are two types of CumSum charts:

1. One two-sided CumSum charts
2. Two one-sided CumSum charts

Two-Sided CumSum

In two-sided CumSum charts, we use a V-mask to identify out-of-control data points. The V-mask is a transparent overlay shape of a horizontal “V” applied on the top of the CumSum chart. Its origin point is placed on the last data point of the CumSum chart and its center line is horizontal. If all of the data points stay inside the V-mask, we consider the process is in statistical control.

V-Mask

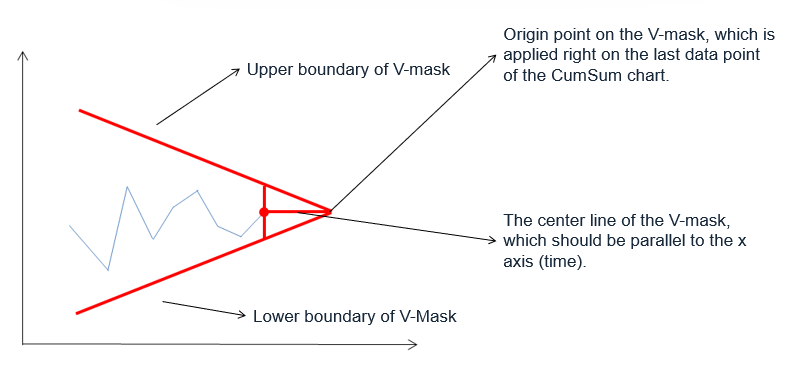
The origin of the V-mask is the most recent data point, and the arms extend backward. The process is out of control if data points fall above or below the limits.

Two-Sided CumSum Equations

Data Point:

V-Mask Slope:

V-Mask Width at the Origin Point:

Where:

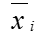•  is the mean of the i^th subgroup
• T is the process target
• σ is the estimation of process standard deviation
• m is the subgroup size

One-Sided CumSum

We can also use two one-sided CumSum charts to detect the shift of the process mean from the process target. The upper one-sided CumSum detects the upward shifts of the process mean. The lower one-sided CumSum detects the downward shifts of the process mean.

One-Sided CumSum Equations

Data Point:

Center Line: T

Upper Control Limit:

Lower Control Limit:

Where:

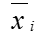•   is the mean of the i^th subgroup
• T is the process target
• σ is the estimation of process standard deviation
• m is the subgroup size

Use JMP to Plot a CumSum Chart

Data File: “CumSum.jmp”

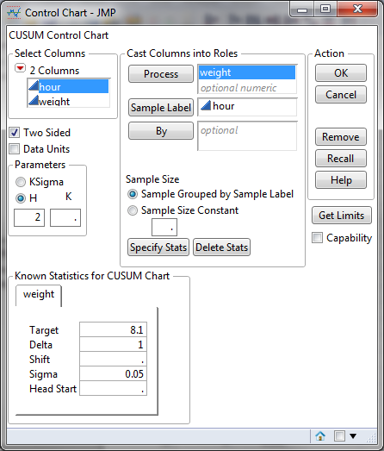
Steps in JMP to plot CumSum charts:

1. Analyze -> Quality & Process -> Control Chart -> CumSum
2. Select Weight in the Process Field
3. Select hour in the Sample Label Field
4. Be sure the check “H” radio button
5. Enter 2 for the H parameter
6. Specify Stats
   a. Enter 8.1 for Target
   b. Enter 1 for Delta
   c. Enter 0.05 for Sigma
7. Click Ok
   

CumSum Chart Diagnosis

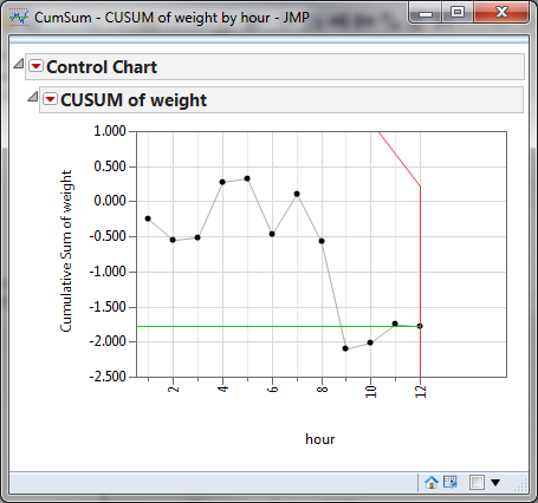
Model summary: The process is in control since all of the data points fall between the two arms of the V-mask.