Box Plot with Minitab

What is a Box Plot with Minitab?

A box plot with Minitab is a graphical method to summarize a data set by visualizing the minimum value, 25th percentile, median, 75th percentile, the maximum value, and potential outliers. A percentile is the value below which a certain percentage of data fall. For example, if 75% of the observations have values lower than 685 in a data set, then 685 is the 75th percentile of the data. At the 50th percentile, or median, 50% of the values are lower and 50% are higher than that value.

Box Plot Anatomy

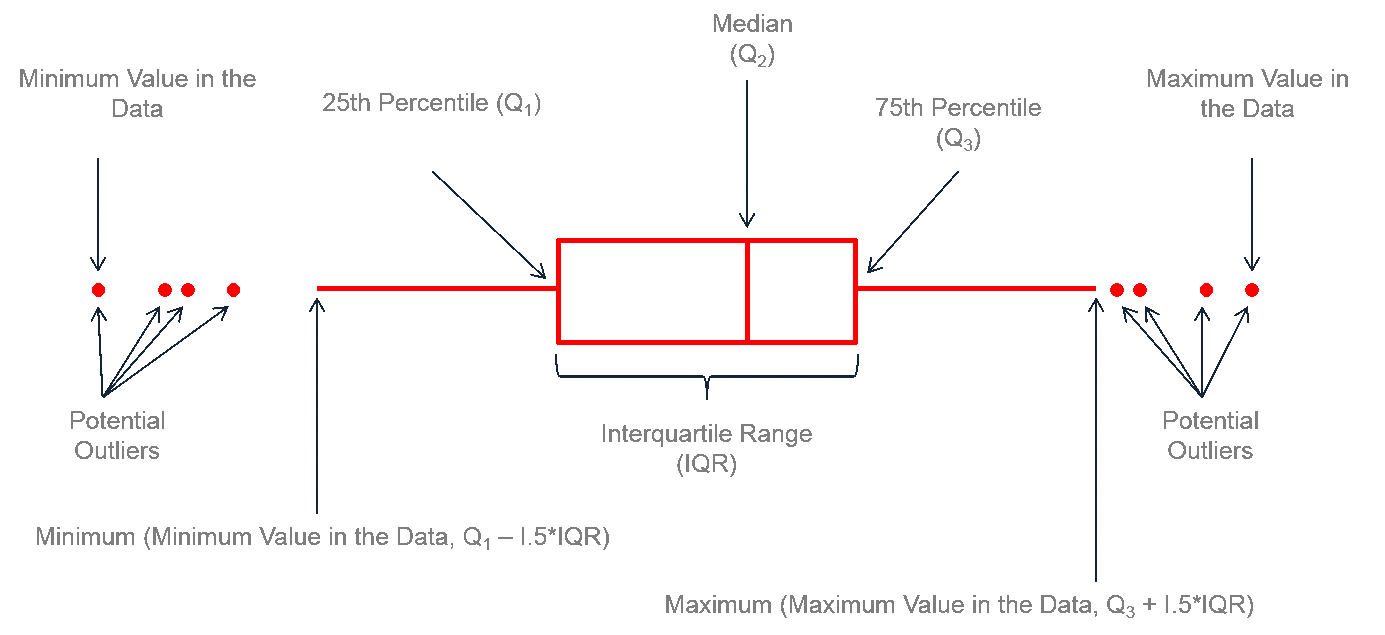The figure above describes how to read a box plot. Here are a few explanations that may help. The middle part of the plot, or the “interquartile range,” represents the middle quartiles (or the 75th minus the 25th percentile). The line near the middle of the box represents the median (or middle value of the data set). The whiskers on either side of the IQR represent the lowest and highest quartiles of the data. The ends of the whiskers represent the maximum and minimum of the data, and the individual dots beyond the whiskers represent outliers in the data set.

How to Use Minitab to Generate a Box Plot

Data File: “Box Plot” tab in “Sample Data.xlsx”

Steps to render a box plot in Minitab:

1. Click Graph → Boxplot.
2. A new window named “Boxplots” pops up.
   
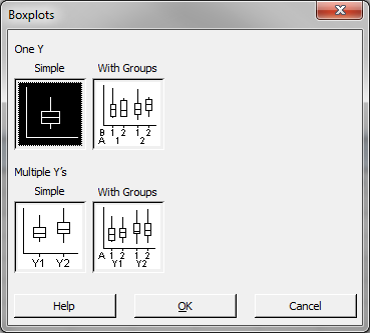
3. Click “OK” in the window “Boxplots.”
4. Another new window named “Boxplot– One Y, Simple” pops up.
   
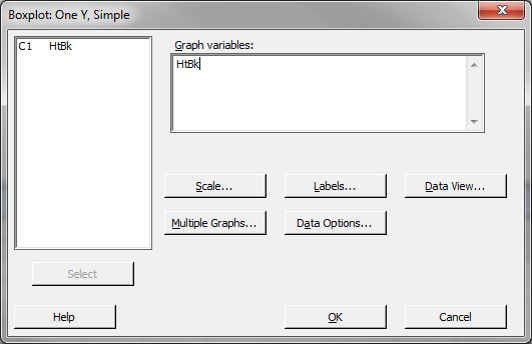
5. Select “HtBk” as the “Graph Variables.”
6. Click the “Data View” button and a new window named “Boxplot– Data View” pops up.
7. Check the boxes “Mediansymbol” and “Mean ”
8. Click “OK” in the window “Boxplot– Data View.”
   
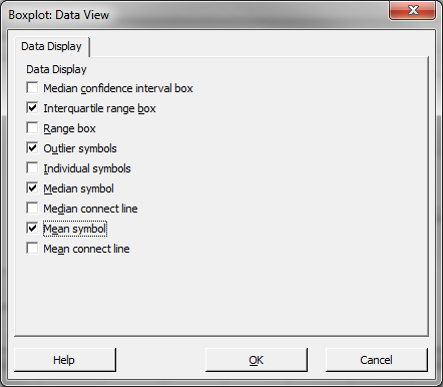
9. Click “OK” in the window “Boxplot– One Y, Simple.”
10. The box plot appears automatically in the new window.
    

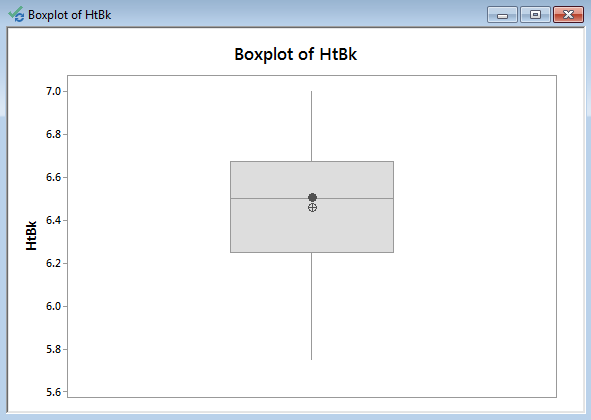
Model summary: The above figure demonstrates the result of the boxplot after navigating through the Minitab menus to yield this output. Notice the interquartile range between the 25^th and 75^th quartiles, the median line, the mean, and the whiskers.